728x90
반응형
- Hermite Spline : Path Smoothing, Interpolation에 사용 가능한 다항식
- 점과 점을 연결하면서, 각 점에서의 기울기를 반영하는 부드러운 곡선 생성
- 3차 다항식 곡선 (Cubic Spline Curve) 형태 -> y = ax^3 + bx^2 + cx + d
- 3차 다항식 곡선 = 변수 4개 -> 4개의 수식 필요
- 2개 점의 위치 값, 2개 점에서의 기울기(1차 미분 값) 4개의 Constraint를 사용하여 계산
Hermite Spline을 사용했을 때 기대대는 효과는 아래와 같다.

파란점선은 4개의 포인트를 직선으로 연결한 선이다. 이를 부드럽게 연결하는 곡선을 만드는 것이 목적이다.
각 점의 포인트와 기울기를 안다면 2개 점을 연결하는 3차곡선을 생성할 수 있다.
이를 각 점마다 (piecewise) 3차곡선을 생성해준 후 연결한다. 이것이 Hermite Spline이다.
아래는 Matlab으로 작성한 Hermite Spline 3차 곡선 계수 계산 로직이다.
4개의 Constraint를 가지고 연립 방정식을 푸는 것이기 때문에, 수식으로 정리하였다.
function [a, b, c, d] = HermiteSplineCoeffi(x_0, y_0, y_der_0, x_1, y_1, y_der_1)
X_1 = x_1 - x_0;
X_2 = x_1 * x_1 - x_0 * x_0;
X_3 = x_1 * x_1 * x_1 - x_0 * x_0 * x_0;
Y = y_1 - y_0;
dY = y_der_1 - y_der_0;
a = ( (Y/X_1) - y_der_0 - (dY/(2 * X_1)) * ( (X_2/X_1) - 2 * x_0) ) / ( (X_3/X_1) - 3 * x_0 * x_0 - (1.5 * X_2 / X_1)* ((X_2/X_1) - 2 * x_0));
b = (dY / (2 * X_1)) - 1.5 * (X_2/X_1) * a;
c = y_der_0 - 3 * a * x_0 * x_0 - 2 * b * x_0;
d = y_0 - a * x_0 * x_0 * x_0 - b * x_0 * x_0 - c * x_0;
end
그런데 Hermite Spline의 단점이 존재한다.
Hermite Spline은 3차곡선이기 때문에 반드시 변곡점이 1개 존재한다. 변곡점은 곡선의 오목/볼록이 변화하는 구간이다.
두 점에서 각 기울기 차이가 크지 않다면, 부드럽게 연결되는 3차곡선이 생성된다.
하지만 두 점에서의 기울기 차이가 크면, 튀는 곡선이 생성된다.
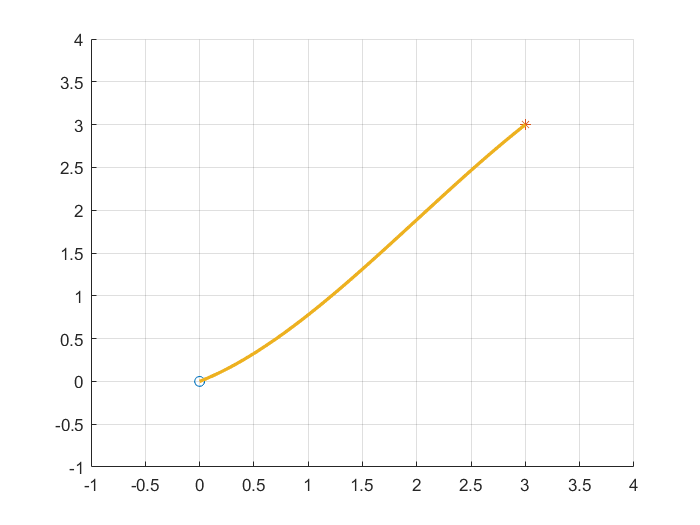

따라서 Smoothing 하려는 두 점의 기울기 차이가 크다면 부드럽지 않은 곡선이 생성된다. 결국 Hermite Spline은 두 점의 기울기가 크지 않은 경우에 사용가능하다.
728x90
반응형
'개념공부 > AD_PlanningAndControl' 카테고리의 다른 글
| Clothoid (0) | 2022.11.02 |
|---|---|
| A* (A star 경로 계획 알고리즘) (0) | 2022.10.31 |
| Review of Motion Planning (1) | 2021.07.11 |
| Corridor Map Method(CMM) Path Planning (1) | 2021.04.08 |
| Path Smoothing 공부해보기 (1) | 2020.09.29 |