강화학습은 인공지능의 한 분야로 분류된다. 강화학습이라는 단어를 뜯어보면 강화 + 학습으로 나누어진다. 즉, 강화학습은 학습을 하는 주체가 있고, 학습을 하는 이유는 무엇인가를 강화하기 위함이라고 생각해볼 수 있다.
강화학습은 어떤 환경(Environment)에서 어떤 주체가(Agent) 최대의 보상(Reward)를 얻을 수 있도록 정책(Policy)을 학습하는 기법을 일컫는다. 여기서 환경과 주체는 현실에서 주어지는 문제이고, 보상은 개발자가 정의하는 것 그리고 정책은 주체가 보상을 받도록 하는 행동을 결정하는 기준을 말한다.
강화학습도 여타 다른 알고리즘과 같이 현실의 문제를 해결하기 위한 도구이다. 강화학습을 현실 문제를 풀 기위한 도구로 사용하는데 있어, 가장 기본 배경 개념은 Markov Decision Process (이하 MDP) 이다. 강화학습을 풀었다 라는 의미는 MDP를 풀었다 와 의미가 동일하다. 따라서 MDP 그리고 Markov Property, Markov Process, Markov Chain, Markov Reward Process, Markov Decision Process과 같은 관련 개념을 정확히 알아둘 필요가 있다. 가장 기본 개념부터 하나씩 정리해보자.
Markov 개념들 중 가장 기본은 Markov Property이다. '어떤 상태 s_t는 Markov 하다'와 같이 사용되는 개념이다. Markov Property의 정의는 현재 상태 s_t만 알면, 과거(s_t-1, s_t-2, ..., s_0)를 아는 것과 동일하게 미래(s_t+1)를 추론할 수 있다는 것이다. 다시 말해 미래 상태는 과거와 관계 없이 현재 상태만으로 결정될 수 있다 는 뜻이다. 이를 수학적으로 정의하면 다음과 같다.
(수식은 다음에..)
다음에 살펴볼 개념은 Markov Process (= Markov Chain, 이하 MP), Markov Reward Process (이하 MRP), Markov Decision Process (이하 MDP)이다. 이 3개의 개념은 문제를 푸는 알고리즘이 아니라 문제를 정의하는 포맷이다.
MP는 <S, P> 튜플로 정의하는 것이다. S : State, P : State transition Matrix이다.
MRP는 MP에서 Reward와 Discount rate가 추가된 것이다. <S, P, R, γ > 튜플로 정의된다.
R : reward (어떤 state에서 state transition에 따라 받게 되는 것), γ : discounted rate (0 ~ 1), 감가율
MRP에서는 Return이라는 개념이 정의된다. Return은 현재 state에서 state transition에 따라 받게되는 reward와 discounted rate가 고려된 값으로, 직관적으로 미래에 받게될 보상들의 합의 현재 값을 의미한다. 이때 discounted rate를 고려하는 이유는 2가지이다. 첫번째는 Return이 무한적으로 커지는 것을 방지하는 것이다. 두번째는 현재 시점에서 먼 미래는 불확실하기 때문에 현재 상태와 가까운 미래에 더 높은 점수를 주는 철학을 반영하는 것이다. (보통 discounted rate는 0과 1 사이의 값을 취하지만, Episode가 반드시 종료되는 환경에서는 1을 사용하기도 한다.)
MRP로 정의된 문제에서 풀고자 하는 것은 (얻고자 하는 답) 상태 가치함수 (이하 State Value function)이다. State Value Function은 현재 state에서 얻을 수 있는 Return의 기댓값으로 정의된다. MRP 문제를 푼다는 것은 현재 상태에서의 State Value function을 계산한다는 것과 동일하다. 이를 계산하기 위해 Bellman Equation을 사용한다. Bellman Equation은 벡터형태의 선형 연립 방정식 표현이 가능하기 때문에 역행렬을 계산하여 직접 해 계산이 가능하다.
MDP는 MRP의 정의에서 agent의 Action이 추가된 것이다. <S, P, A, R, γ > 튜플로 정의된다. A : Action at State
MDP로 정의되는 상황은 Agent가 어떠한 state에서 action을 결정하고 state transition matrix에 따라 다음 state로 천이된 후 Reward를 얻는 상황이다. 이때 state transition matrix, p는 MRP에서의 정의와 조금 달라지는데, 특정 state에서 특정 action을 행했을 때 특정 state로 전환될 확률을 의미한다. 즉, 특정 state에서 Action을 결정하는 기준이 있다는 것이고 이 기준을 정책(이하 Policy)라고 지칭한다. Policy와 state transition의 개념이 조금 헷갈릴 수 있는데, Policy 는 특정 state에서 Action을 선택할 확률, state transition은 특정 state에서 특정 action을 행했을 때 특정 state로 전환될 확률이다. 다시 말해 특정 state에서 특정 action을 행했을 때의 결과가 결정론적이지 않고 확률적임을 의미한다.
MDP에서는 Action이 추가된 상황이기 때문에, MRP의 State Value function에서 Action이 추가된 Action value function의 개념이 존재한다. 이는 특정 state에서 특정 action을 행했을 때 얻을 Return의 기댓값이다. (value function은 특정 state에서 얻는 Return의 기댓값이다.)
MDP 문제를 푸는 것은 State Value function과 Action Value function을 최대화 하는 Policy를 찾는 것이다. 이는 곧 최적 Policy를 찾는다 라고 말할 수도 있다. (참고로, MDP에서는 최적 Policy가 유일하지 않을 수 있다.)
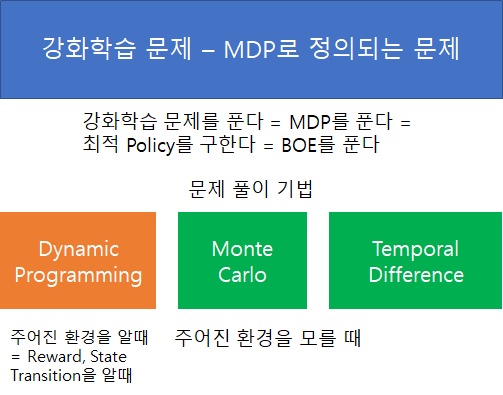
앞서 MRP 문제를 풀때는 Bellman Equation을 사용했다. 이때 Bellman Equation은 선형 방정식이었기 때문에 직접해를 계산할 수 있었다. MDP에서는 Bellman Optimality Equation을 사용하는데, 이는 선형 방정식이 아니다. 따라서 일반해가 존재하지 않는다. MDP를 푸는 방법으로 Policy Evaluation, Policy Iteration, Q-Learning, SARSA 등이 존재한다. 강화학습 문제는 MDP로 정의되기 때문에 위의 방법은 결국 강화학습 문제를 푸는데 사용되는 알고리즘 들이다. 다음 글 부터는 Policy Evaluation, Policy Iteration과 같은 주어진 환경을 아는 상황에서 문제를 푸는데 사용되는 Dynamic Programming에 대해 정리해볼 것이다.
'개념공부 > 강화학습(Reinforcement Learning)' 카테고리의 다른 글
| 강화학습 5 <Policy-based RL의 시작 : REINFORCE> (1) | 2021.12.26 |
|---|---|
| 강화학습 4 <인공신경망을 활용한 강화학습 - Deep SARSA> (0) | 2021.12.24 |
| 강화학습 3 <환경을 모를때 MDP 풀이, MC, TD, SARSA, Q-Learning> (0) | 2021.12.01 |
| 강화학습 응용 <DP를 활용한 교차로 우회전 경로 생성> (0) | 2021.11.30 |
| 강화학습 - 2 <MDP를 푸는 Dynamic Programming 기법> (0) | 2021.11.28 |

