728x90
반응형
선형대수에는 여러가지 분해 종류가 있는데, 대표적으로 직교벡터분해, QR분해, LU분해, 고윳값분해, 특잇값분해가 있다. 분해란 벡터나 행렬 하나를 2개 이상으로 분리하는 것을 말한다. 직교벡터분해의 경우 아래 페이지에 정리하였으니 참고하자. (https://iridescentboy.tistory.com/160)
본 페이지에서는 직교행렬과 QR분해를 다룬다. 중심이 되는 것은 QR분해이고, 이는 역행렬, 최소제곱모델적합, 고윳값 분해등에 사용되는 중요한 개념이다.
직교행렬 (Orthogonal Matrix)
- 직교행렬은 다음 2가지 특징을 가진 행렬이다.
- 행렬의 모든 열은 서로 직교한다. = 내적 시 0 이다.
- 각 열의 Norm은 1이다.
- 이를 수식으로 표현하면 다음과 같다.
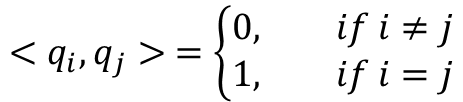
- 이를 행렬 관점에서 보면, 어떤 행렬 Q와 전치 행렬을 내적했을 때 단위 행렬이 되는 것과 동일하다.
- 이는 직교행렬의 역행렬은 전치 행렬과 동일함을 뜻한다.
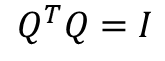
- QR분해 내용을 미리 말하자면, QR분해 시 도출되는 Q행렬은 직교행렬이다.
그람-슈미트 과정
- 그람-슈미트 과정은 비직교행렬 A를 직교행렬 Q로 만드는 알고리즘이다.
- 본 과정은 나눗셈과 곱셈 연산이 많아서, 수치적으로 불안정한 특징이 있다.
- 일반적으로 직교 행렬을 생성할 때는, 그람-슈미트보다 하우스홀더 변환(Householder reflection)을 많이 쓴다.
- 그람-슈미트 과정의 알고리즘은 다음을 참고하자. (작성 예정)
QR 분해
- QR분해는 행렬 A를 직교행렬인 Q와 일반 행렬 R의 곱으로 분해한다.
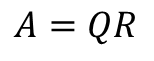
- 이때 직교행렬 Q를 구하는 방법으로는 그람-슈미트 과정, 하우스홀더 변환 방법 등이 있다.
- 행렬 R은 행렬 Q를 구한 이후, 아래의 방법으로 계산한다.
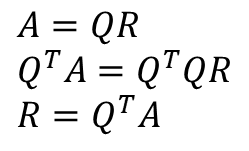
- 행렬 R은 항상 상삼각행렬이다.
QR 분해의 활용
- QR분해는역행렬, 최소제곱모델 적합, 고윳값 분해 등에 사용되는 중요한 선형대수 개념이다.
- 본 페이지에서는 QR 분해를 사용해 역행렬을 계산하는 예시만 살펴보자.
- 일반적으로,행렬 A의 역행렬을 계산 시, 2x2 행렬, 3x3 행렬에 대해 Determinant를 사용해 계산한다.
- 본 방법은 Determinant가 0일 때 계산이 안되고, 곱셈과 나눗셈이 있어 수치적으로 불안정해질 수 있다.
- QR 분해를 사용하면 위의 방법보다 수치적으로 조금 더 안정적으로 역행렬을 계산할수 있다.
- QR 분해를 이용해 A의 역행렬은 아래와 같이 계산한다.
- 일반적으로,행렬 A의 역행렬을 계산 시, 2x2 행렬, 3x3 행렬에 대해 Determinant를 사용해 계산한다.
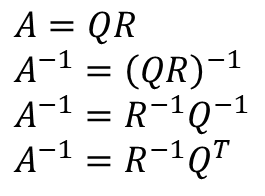
- 위 과정에서 Q는 직교행렬이기 때문에, Q의 역행렬은 전치행렬과 동일하다.
- R의 역행렬을 계산해야 하는 과정이 남아 있는데, R은 상삼각 행렬이기 때문에 역행렬 계산 시 수치적으로 안정적이다. (A 행렬의 역행렬을 계산하는 것에 비해)
- 결과적으로, QR 분해를 사용하면 Determinant를 사용해 역행렬을 계산하는 것보다 수치적으로 안정적이게 역행렬을계산할 수 있다. 하지만 QR 분해를 사용한 역행렬 계산 과정은 상대적으로 안정적이다는 것이지, 모든 행렬에 대해 수치 안정성을 제공하는 방법은 아니다.
728x90
반응형
'개념공부 > 선형대수' 카테고리의 다른 글
| [선형대수] 일반선형모델 및 최소제곱법 (0) | 2024.01.15 |
|---|---|
| [선형대수] 행 축소와 LU 분해 (0) | 2024.01.15 |
| [선형대수] 행렬 계수란(Rank) (1) | 2024.01.05 |
| [선형대수] 행렬 Norm, 행렬공간 (1) | 2024.01.05 |
| [선형대수] 직교벡터 분해 (0) | 2023.12.31 |

