Heap, 힙
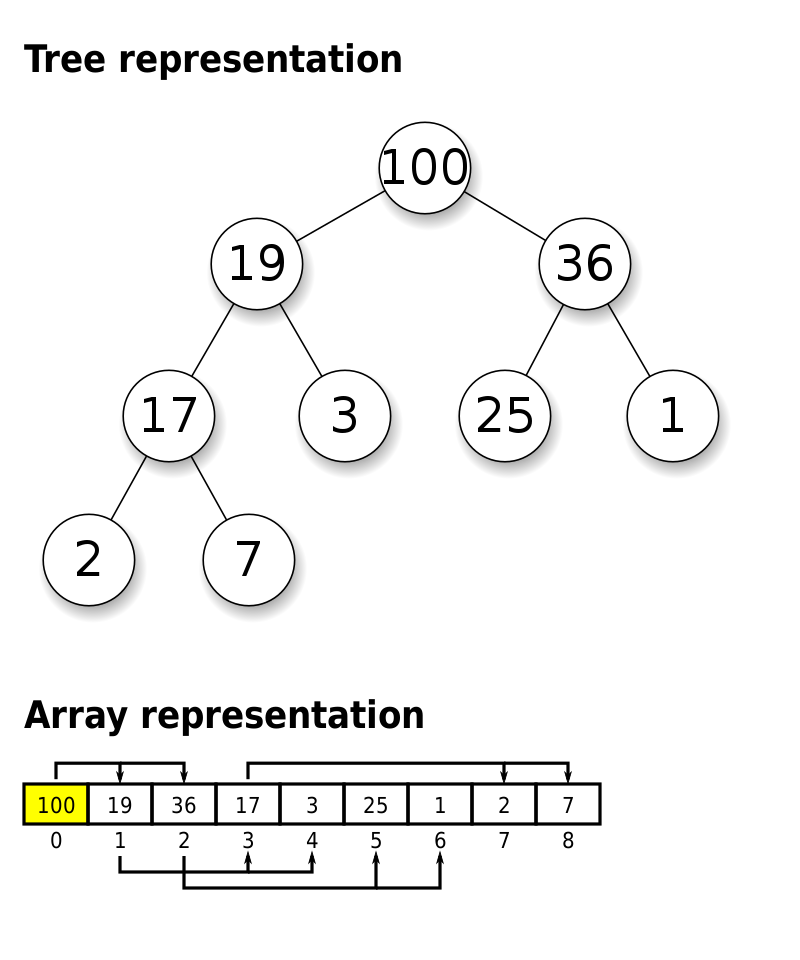
힙(heap)은 힙 속성을 만족하는 tree를 기반으로하는 자료구조 이다. 힙 속성은 다음과 같다. A가 B의 부모 노드라면, A 노드의 값은 B 노드의 값과 대소 관계가 성립한다. 이때, 부모 노드가 자식 노드보다 값이 크다면 '최대 힙', 반대라면 '최수 힙'이라고 지칭한다. 각 노드 간의 대소 관계는 오직 부모 노드와 자식 노드 간에만 성립되고, 형제 노드 사이에는 대소 관계가 정해지지 않는다.
힙은 자식 노드의 최대 개수에 따라 종류가 나니ㅜ는데, 보통은 자식 노드가 2개인 이진 힙 (Binary tree)에 사용한다. 힙을 사용하는 이유는 배열에서 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위함이다. 힙은 가장 큰 값 (혹은 가장 작은 값)이 Root 노드에 오는 특징이 있고, 이를 활용해 우선 순위 큐 (Priority Queue)와 같은 자료 구조를 구현한다.
힙의 시간 복잡성은 O(log n) 이다.
연산
힙 자료구조는 일반적으로 Make_heap(), pop_heap(), push_heap(), sort_heap() 연산을 가진다. (C++ 기준으로 <Algorithm> 헤더에 포함되어 있다.)
1. make_heap() : Container를 Heap 속성을 가지는 힙 자료구조로 만드는 함수이다.
2. pop_heap() : heap 자료구조에서 가장 큰 (혹은 가장 작은) 값, 즉 Root 노드의 값을 자료 구조의 가장 마지막 인덱스로 보낸다. (자료구조에서 해당 값을 삭제하려면, pop_back()을 호출 해야 한다.)
3. push_heap() : 힙 자료구조의 가장 마지막 인덱스 - 1의 위치에 요소를 삽입한다. 이후 힙 속성을 유지하기 해서는 make_heap()를 호출해야 한다.
4. sort_heap() : 힙 자료구조에서 elements를 정렬한다. (make_heap()과의 차이점은, make_heap()은 container를 입력 받아 힙 속성을 유지하는 자료구조로 만드는 것이고, sort_heap()은 힙 자료구조를 입력 받아 정렬하는 것이다.)
사용 예제
보통 힙은 우선순위 큐 자료 구조를 구현하는데 사용된다. 그 밖에도 Container에서 N번째로 큰 (혹은 작은) 원소를 찾는데 사용될 수 있다. 일반적으로 Container에서 크기에 따른 값을 찾을 때는 정렬 -> 특정 인덱스 접근 순서로 실행된다. 하지만 Heap 자료구조는 Container를 정렬하는 연산을 대체하여 사용될 수 있다.
힙의 시간 복잡성이 O(log n)이므로 O(n^2)인 정렬보다 더 빠르게 수행될 수 있음을 알 수 있다.
관련 예제
LeetCode 215. Kth Largest Element in an Array 문제를 풀어보자
Kth Largest Element in an Array - LeetCode
Can you solve this real interview question? Kth Largest Element in an Array - Given an integer array nums and an integer k, return the kth largest element in the array. Note that it is the kth largest element in the sorted order, not the kth distinct eleme
leetcode.com
Container에서 N번째로 큰 원소 값을 찾는 문제인데, 정렬(sorting)없이 문제를 풀어야 한다.
'개념공부 > 알고리즘' 카테고리의 다른 글
| 배열에서 연산의 최댓값 혹은 최솟값을 가지는 2개의 값 찾기 문제 (Two Pointers) (0) | 2023.08.01 |
|---|---|
| Container에서 최댓값 (최솟값) 혹은 N번째 최댓값 (최솟값) 찾기 (0) | 2023.07.30 |
| Interval, Scheduling 문제 (LeetCode 435) (1) | 2023.07.28 |
| Fibonacci(피보나치), Tribonacci 문제 풀이 DP, Recursion, Bottom Up (0) | 2023.07.27 |
| Monotonic Stack, 단조 스택이란? (1) | 2023.07.24 |